지시사항
신호가 당신에게 닿는데 걸리는 시간은 밀리 초(ms) 단위로 나타나있다(1000ms = 1s).
전파 신호는 빛의 속력으로 전달된다. 따라서 시간을 거리로 변환하기 위해서 빛의 속력은 일정(c = 299792.459km/s)하게 사용되어야 한다.
예:
측정된 신호 전달 시간이 10ms라고 가정하자. 인공위성까지 측정된 거리는 다음을 이용해서 계산할 수 있다.
s = c • t
s: 인공위성까지의 거리
c: 빛의 속력
t: 신호 전달 시간
s = 299792.458km/s • 10ms = 299792.485km/s • 0.01s = 2997.92km
학생들에게 항상 시간을 밀리 초에서 초 단위로 변환해야한다고 지도한다.
지도에서 축적이란 무엇인가?
첫 번째 단계에서 지도의 축적을 결정했다. 이것은 가능하면 정확해야한다. 선은 300km를 나타낸다. 중요: 활동지의 지도에서 축적을 변경하지 마라. 육지에서 300km는 지도에서 13mm를 의미한다.
인공위성까지 얼마나 떨어져있는가?
학생들에게 활동지에 있는 표(표 1)의 빠진 값을 채워 넣어야 한다고 설명한다. 이번 활동에서 이 부분은 ‘측정값(measured)’이라고 적힌 열만 사용할 수 있다. ‘수정값(corrected)’이라고 적힌 열은 심화학습 단계의 학생들에게 필요한 것이다(아래 참고).
표 1 : 활동지 2에 제시된 표
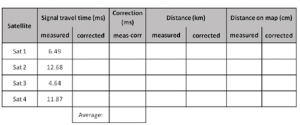
이제 학생들은 수신기에 나타난 시간(표 참고)으로 전달된 신호의 거리를 추정한다. 단위를 고려하면 시간은 상수인 빛의 속력(299792.458km/s)을 곱해야한다. 계산된 값은 ‘거리(Distance, km), 측정값(measured)’의 열에 기입한다.
학생들은 지도의 축적을 이용하여 이 거리를 지도상의 거리로 변환한다. 이전에 언급했듯이 지구상 300km는 지도상 13mm와 같다. 이 값은 ‘지도상 거리(Distance on map, cm), 측정값(measured)’ 열에 기입한다. 결과 값은 표 2에 나타나있다.
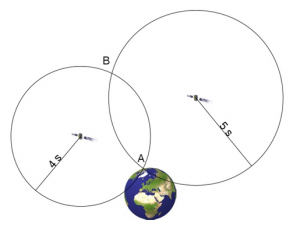
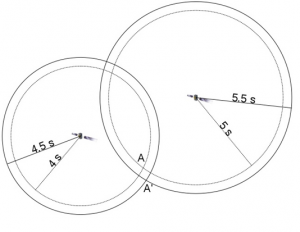
다음으로 학생들은 컴퍼스를 이용하여 신호 전달 거리에 해당하는 반지름을 가진 원이나 원호를 그린다. 각 원호를 추가하면 학생들은 자신의 국가를 결정할 수 있을 것이다.
질문: 각각의 추가된 인공위성 신호의 원호로부터 자신이 있을 것으로 생각하는 위치에 대해 알아낸 것이 있나요?
답: 각 인공위성 원호를 추가하면서 위치가 좀 더 정밀하게 결정됩니다.
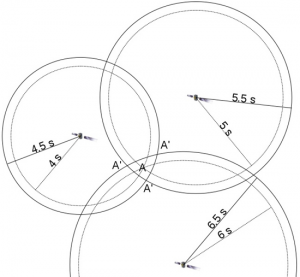
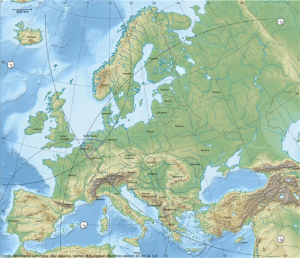
마지막 인공위성의 원호를 그리면 학생들은 4개의 원호가 하나의 점에서 교차하지는 않지만 그 영역은 실제 위치를 포함해야한다는 것을 알게 될 것이다(그림 9). 이것은 수신기 시계의 문제이다. 정확한 위치는 교차점으로 둘러싸인 영역의 어느 한 곳이다.
질문: 여러분의 현재의 위치로 추정되는 나라는 어디인가요?
답: 가능성 있는 곳은 네덜란드, 벨기에, 룩셈부르크, 독일입니다.
그림 9: 람베르트 정적 방위도법으로 나타낸 유럽 지도. 원호는 활동지 2의 표에서 명시된 시간 안에 4개의 인공위성으로부터 전달된 신호의 거리를 나타내는 것이다(출처는 그림 7 참고).
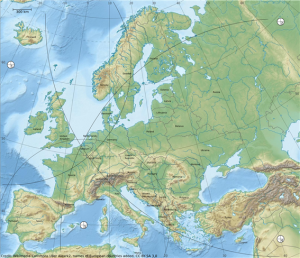
위치를 좀 더 정확하게 결정하기 위해서(아래 확장 활동을 준비한다면) 하나의 점이 실제 위치를 나타내야한다. 두 가지 접근법을 사용할 수 있다.
단순한 방법
교차점의 결과로 나타난 지역의 질량 중심은 4개의 원호에서 같은 거리를 가진 지점으로 추정하여 결정될 수 있다. 무게 중심은 네덜란드의 남부 지역이다.
심화 방법
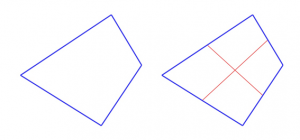
실제로 GPS 수신기는 교차되는 한 지점을 찾을 때까지 혹은 위치가 최대한 작은 지역으로 좁혀질 때까지 시간 오차를 변경한다. 이 알고리즘은 질량 중심에 대한 근사치를 도출하는 활동으로 단순화될 수 있다. 일반적인 영역은 4개의 원호로 둘러싸여 있다. 학생들은 각각의 이등분선을 알아내야한다. 그리고 학생들은 마주보는 선분의 이등분선을 연결한다. 두 선분의 교차점은 질량 중심으로 정의할 수 있다(그림 6). 이것은 실제 위치에 대한 좋은 접근이다. 다시 그 위치는 네덜란드의 남부 지역이다(그림 10).
그림 10: 이전과 같은 지도이지만 이번에는 모형으로 계산된 지점에 대한 근사치를 사용한다(출처는 그림 7 참고).
심화 과정 학생들을 위한 확장 활동: 시계 수정하기
질문: GPS 측정값으로 얻은 거리와 내삽법으로 결정한 위치가 서로 다른 이유는 무엇일까요?
답: GPS 수신기의 시계가 정확하지 않기 때문입니다.
실제 GPS 수신기에서는 인공위성에 대해 수정하기 위해서 내삽법으로 나타난 위치가 사용된다. 그 후 GPS 수신기는 차후 위치를 추정한다. 이번 추가 활동은 이러한 계산을 보여주고 수신기 시계의 오차를 결정한다.
교차된 지역의 질량 중심을 결정한 후(그림 10) 학생들은 지도에서의 인공위성간의 거리를 측정한다. 그 값은 활동지 표의 ‘지도상 거리(distance on the map, cm), 수정 값(corrected)’이라고 적혀있는 열에 기입한다. 이 값을 지도의 축적을 이용하여 실제 거리로 변환하고 ‘거리(distance, km), 수정 값(corrected)’이라고 쓰여 있는 열에 기입한다.
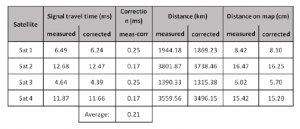
각 인공위성의 수정된 신호 전달 시간은 빛의 속도를 이용해서 계산하고 이를 ‘신호 전달 시간(Signal travel time, ms), 수정 값(corrected)’에 해당하는 열에 기입한다. 이를 통해 학생들은 모의 실험된 GPS 수신기에 의해 주어진 초기 값과 수정 값 사이의 차이를 계산한다. 이러한 차이는 ‘수정 값(Correction, ms), meas-corr’ 열에 기입한다. 서로 다른 4개의 결과 값으로부터 학생들은 평균을 도출할 수 있다. 이것은 모의실험에 사용된 GPS 수신기에 적용되는 시계의 추가 보정 값이다. 결과 값은 표 2에 나타난 것과 비슷할 것이다.
표 2: 결과 값이 나타난 표.
 목적
목적 학습 목표
학습 목표 평가
평가 준비물
준비물